23 ecke - Georg Nees
More searching for seeds
Having replicated Georg Nees’ iconic 1968/69 work, “Schotter”, I turned my attention to his “23 ecke” (literally “23 corners”, usually referred to as “Polygons of 23 vertices”), an earlier work from 1964:
Background

23 ecke (“Polygon of 23 Vertices”) — Georg Nees, 1964
(Version published in rot 19 in 1965)
From the 5th to the 19th of February, 1965, the world’s first exhibition of digital art was staged in the Studiengalerie of the University of Stuttgart. Georg Nees displayed a dozen or so drawings on the walls, and in the accompanying nineteenth edition of Max Bense’s booklet series rot (“red”), Nees provided short descriptions in his usual clear style. 23 ecke was one of the works displayed, and described in rot 19.
My description of the 1965 show is drawn from Frieder Nake’s short paper, Computer Art. A Personal Recollection.1 I recommend it: his account of the reactions of other artists and musings on “artificial art” (as Bense coined it) are fascinating.
The pure visual appearance of the drawings was not too exciting. One could easily ignore them, if one wanted to. The challenge really came from the principle that emerged. It was outrageous. It may have appeared as if conceptual art was left way behind but, at the same time, its idea gained a new kind of power. The schema, the structure, the class properties of entire sets of drawings were described and given to the machine for it to work out the details. The individual work became part only of a generative schema. Aesthetics was confronted by a new task, and the artist was threatened in his or her very existence. The individual realization on the wall no longer carried the essence of art. Art now had become the class of works which the picture belonged to. That class consisted most likely of endless chains of variations. — Frieder Nake
Nake refers to “issue no. 19 of the now legendary edition rot”, and indeed, the booklet series–especially rot 19—seems to come up often when reading about digital art. The center of excellence digital art—compart—describes rot 19:
This little booklet of 14 pages is one of the first publications ever on computer art. It appeared at the occasion of the first exhibition of computer-generated algorithmic art world-wide: the famous show of a small set of graphic works by Georg Nees. The show was opened on February 4, 1965, and lasted until February 19, 1965, on the premises of the Studiengalerie of TH Stuttgart (now University of Stuttgart).
For more information on the rot journal, ZKM has an exhibit.
First attempt
At first I thought reproducing 23 ecke was going to be easy, using the experience and resources gained reproducing schotter. In sections 3.2.2 and 3.2.3 of his 1969 thesis, Nees lists the routine, “ELIRR” (ELementaren IRRweg — “elementary random path”2):
1 'PROCEDURE'ELIRR.,
2 'BEGIN'
3 JA1.=P+JLI.,JE1.=P+JRE.,
4 JA2.=Q+JUN.,JE2.=Q+JOB.,
5 P1.=J1.,Q1.=J2.,
6 LEER(P1.Q1).,
7 'FOR'M.=1'STEP'1'UNTIL'N'DO'
8 'IF'T'EQUAL'0'THEN'
9 'BEGIN'
10 LINE(J1,Y).,LINE(X,J2)
11 'END'
12 'ELSE'LINE(J1,J2).,
13 'IF'T'EQUAL'0'THEN'
14 'BEGIN'
15 LINE(P1,Y).,LINE(X,Q1)
16 'END'
17 'ELSE'LINE(P1,Q1)
18 'END'ELIRR.,
3.2.2.
Now that we have the multi-purpose procedure The elementary random walk SERIES, we standardize the figure-drawing procedure that has to replace the formal parameter FIGURE in SERIE. The parameterless procedure ELIRR draws a random walk in a frame rectangle whose corner point coordinates match the interval limits of the random generators J1 and J2. The random walk controlled by J1 and J2 consists of diagonal or axis-parallel sections, depending on whether the integer and global size T agreed in line 5 of the declaration sequence (1/3.2.1) in ELIRR has the value 1 or 0.
We can transliterate this into ALGOL-ish Python:
import drawsvg as draw
def draw_figures(QUER, HOCH, XMAL, YMAL, inset, N, S1, S2, diag=False,
stroke_width=0.3, svg_width=160, svg_height=200):
JLI = inset / 2
JRE = QUER - inset / 2
JUN = inset / 2
JOB = HOCH - inset / 2
x = y = 0
r1 = Random(S1)
r2 = Random(S2)
d = draw.Drawing(svg_width, svg_height, origin='center',
style="background-color:#eae6e2")
g = draw.Group(transform="rotate(180)", stroke='#41403a',
stroke_width=f'{stroke_width}', fill='none',
stroke_linecap="round", stroke_linejoin="round")
def serie(QUER, HOCH, XMAL, YMAL, FIGUR):
P = -QUER * XMAL * 0.5
Q = YANF = -HOCH * YMAL * 0.5
for COUNTX in range(1, XMAL+1):
Q = YANF
for COUNTY in range(1, YMAL+1):
p = draw.Path()
FIGUR(P, Q, p)
g.append(p)
Q = Q + HOCH
P = P + QUER
def elirr(P, Q, p):
JA1 = P + JLI
JE1 = P + JRE
JA2 = Q + JUN
JE2 = Q + JOB
P1 = r1.next(JA1, JE1)
Q1 = r2.next(JA2, JE2)
p.m(Q1,P1)
X, Y = P1, Q1
for M in range(1, N+1):
X = r1.next(JA1, JE1)
p.L(Y, X)
Y = r2.next(JA2, JE2)
p.L(Y,X)
if diag:
p.L(Q1,P1)
else:
p.L(Y,P1)
X = P1
p.L(Q1,X)
serie(QUER, HOCH, XMAL, YMAL, elirr)
d.append(g)
return d
svg = draw_figures(20, 20, 8, 6, 0, 20, JS2, JS5, stroke_width=0.3)
svg.set_render_size(w=500)
The resulting images (reproduced using seeds JS2 and JS5 from the thesis) look similar to those in “23 ecke”, except that the patterns here are a little more tangled, and lack the single diagonal line:
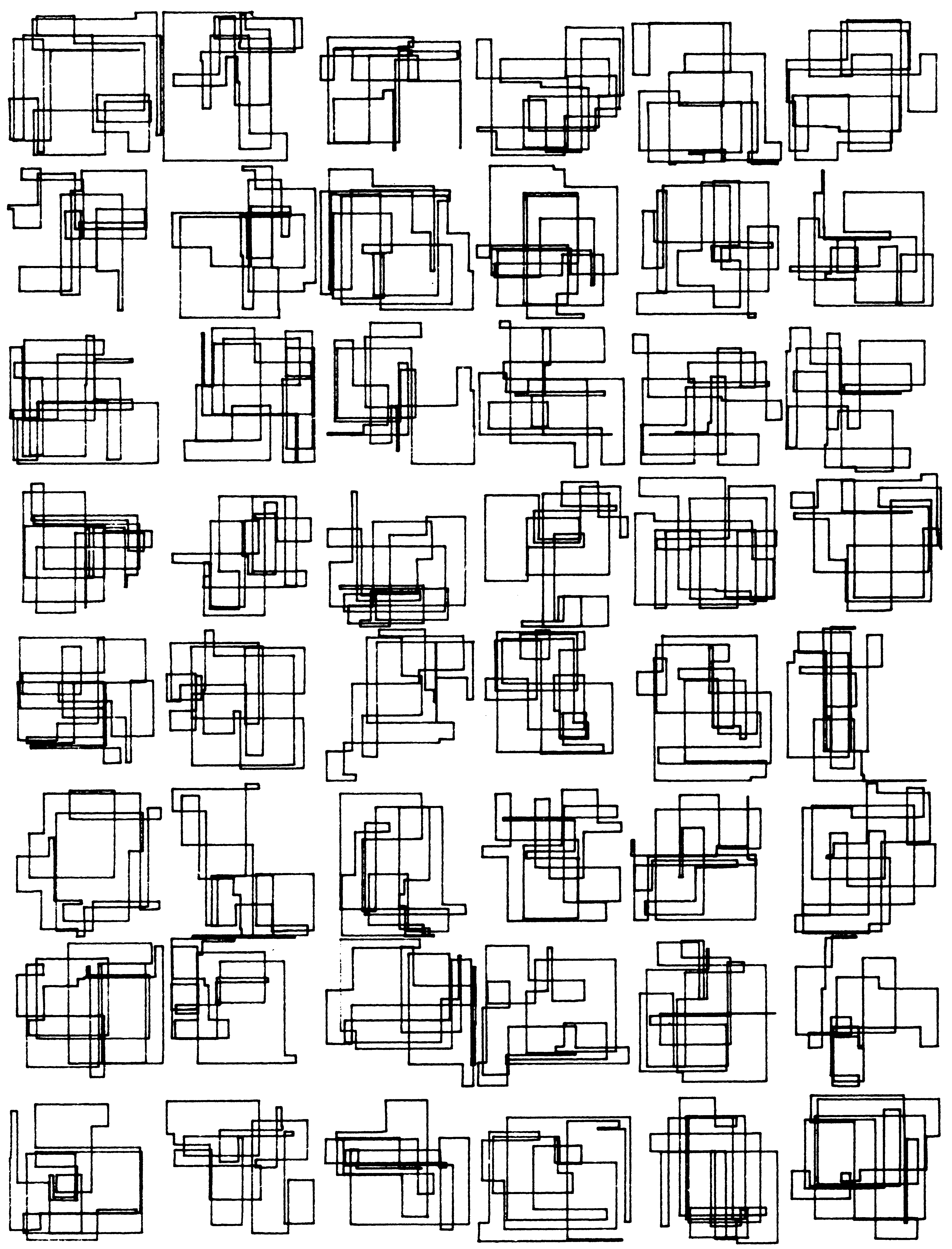
Bild 22 (Picture 22) from Georg Nees’ 1969 thesis
Second attempt
My next step was to start trying to trace out the shapes from 23 ecke, in an attempt to iterate through seeds and find matching shapes:
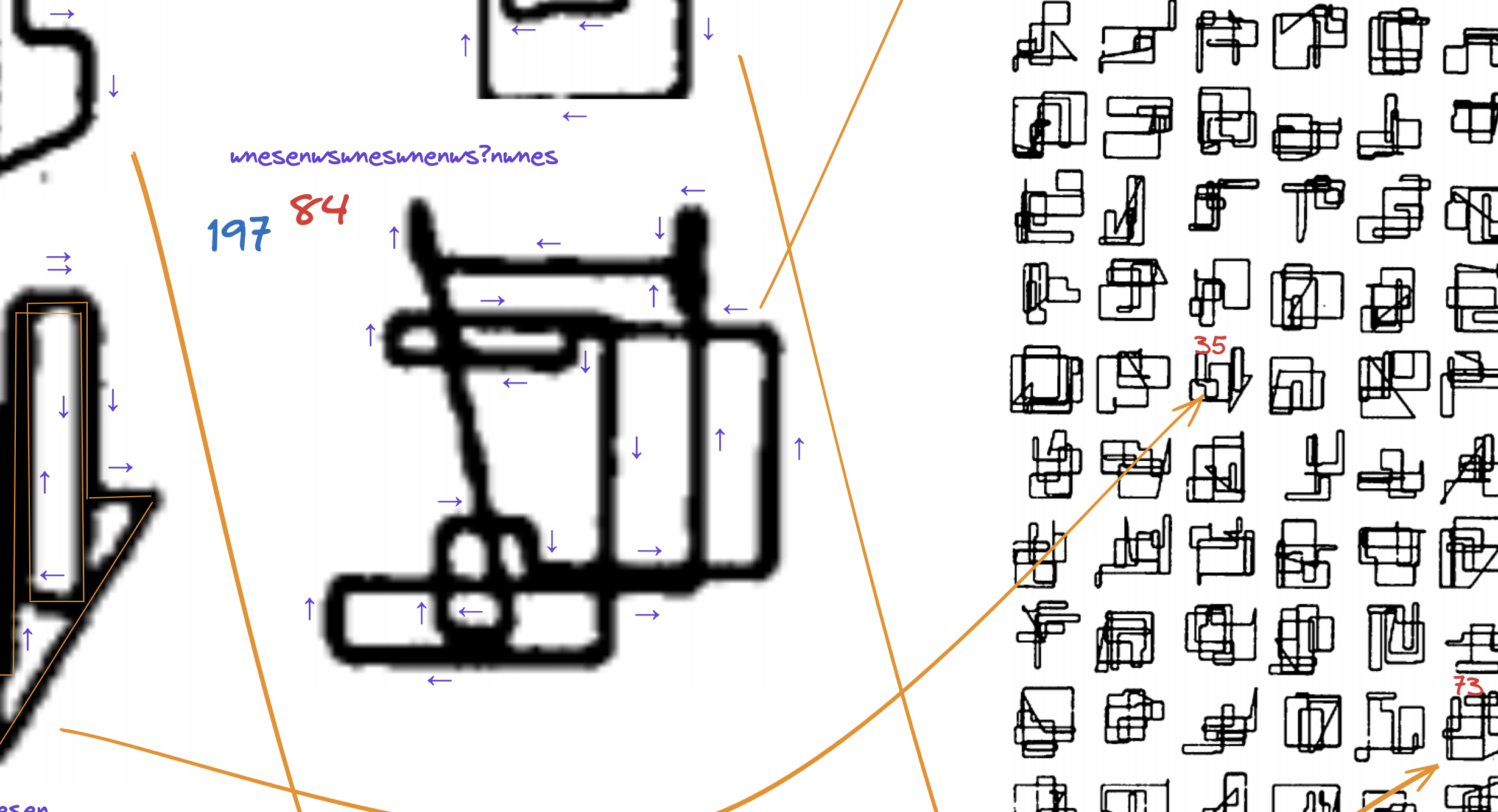
This didn’t work: the shapes were too blurry, and have too much overlap, and despite spending a lot of time on it, I never did feel sure that I had correctly deciphered and transcribed any of them. The long search far and wide for ever higher resolution images of 23 ecke was useful though: I found many of the resources mentioned in this post.
By this time, I had also noticed that the 23 ecke image is sometimes shown with 14x19 shapes (as in rot 19), and sometimes 14x20, and also that its orientation is unclear: from the thesis, it seems that Nees’ plotter drew on paper in what we would consider “landscape mode” but the work is often shown oriented vertically, so I wasn’t even sure in which order the shapes were drawn.
The missing row was explained in a paper called “A Vision without a Sight: From Max Bense’s Theory to the Dialectic of Programmed Images”, by Gaëtan Robillard and Prof. Alain Lioret, from the website of the XXII Generative Art Conference in 2019: it turns out that Max Bense had edited the original image Nees gave him when printing rot 19, removing one row, and also Nees’ name:

Fig2. Georg Nees, 23-Edge: detailed view from editor’s draft, Rot n° 19, 1965. From the Walther-Bense Estate archive at the Center for Art and Media Karlsruhe (ZKM)
I recommend reading that section of the paper, since M. Robillard’s comments and questions about Bense’s editing of the image are thought-provoking.
…it is remarkable that this simple gesture of framing witnesses Bense’s relation to authorship and to the new category of programmed images. …
I find it significant that Bense removed the human touch, and human attribution, of Nees’ name. It seems to fit his presentation of “artificial art”.
I have emailed the curators of the Elisabeth Walther-Bense Archives at ZKM seeking to get a full image of the printer’s draft that I can post online, but haven’t heard back yet.
Luckily, searching at length for a higher-resolution image of 23 ecke, I looked more closely at the (20x14) version in Nees’ preface to the 2006 reprint of his thesis, and noticed that the figure was captioned, “Abb. 4: Georg Nees: Variationen von Figuren in der statistischen Grafik. In: Grundlagenstudien aus Kybernetik und Geisteswissenschaft 5 (1964), H. 3/4, S. 121-125.”
Happily, that 1964 publication is available at archive.org, and even more happily, also contains a description of the algorithm.
Note that rather than two separate random generators, one for the X coordinates and one for the Y, this description uses just one. Perhaps in 1964, Nees had not yet settled as firmly on the approach laid out in his thesis. I now knew that I would probably need to try a few different variations.
Having failed to find the seeds by attempting to correctly annotate movements within shapes, I decided to focus instead on the characteristics of the diagonal lines. By happenstance, I ran across Marimo, a version of Python notebooks that allows easy use of interactive widgets, and was able to whip up a crude interface and manually classify as many of the 280 diagonals as possible.
Even that wasn’t quite enough. After failing to match the images with any of the two billion available seeds, I started trying variations. Apparently, in 1964 Nees was using random numbers modulo 230, rather than 231. Eventually, I had a hit!
Success!
And with that, we have the original image! The seed is 314,748,365, the modulo is 230, and one random generator is used for both X and Y coordinates. Otherwise the code is as described in ELIRR. (My source code is available on github, which will even render the jupyter notebook nicely.)
Recreation of 23 ecke
Final notes, a request, and #followfriday
The real plots are tiny
One fascinating aspect of these images, especially Schotter, is just how small they are. Accustomed as I am to seeing artwork on my computer screen, I assumed Schotter was a foot or two wide. In fact, the area Georg Nees had available to him on his plotter was more like 28-30cm (about a foot) on the long edge. These pictures are tiny!
An unexpected email
I was delighted and surprised to receive an email from one of Georg Nees’ sons! Apparently a colleague sent him a link to my blog posts on Schotter. It was gratifying to hear that they were excited about the reconstruction of his code and images.
Any leads on Vera Molnár source code?
Next, I want to try reproducing early images of another computer artwork pioneer, Vera Molnár. If anyone has leads on source code for any of her artwork, (or lives close enough to her estate to visit her journals) I’d love have a go at modernizing the code and looking for seeds.
Random artist shoutout: Murilo Polese
While looking for information on Vera Molnár, I ran across the Vera Molnár page in the research section on the website for the Recreating the Past course at the intriguing School for Poetic Computation in New York City.
From there, I found the recent leader of that course, Murilo Polese, an astonishing dynamo of creative activity. If you’d like to get inspired by a current computer art practitioner as well as by the early artists, you could certainly lose an afternoon exploring their many projects:
- murilopolese.com
- bananabanana.me gallery
- bananabanana.me random toys and projects
- amazing color programming toy on bananabanana.me
- @[email protected] on Mastodon (fka @murilopolese on twitter)
Ciao!
That’s it for now. Please get in touch — @[email protected] — with any comments, requests, or just to chat.
- Part one: Schotter: Introduction
- Part two: Schotter: Investigation
- Part three: 23 ecke
-
“Computer Art. A Personal Recollection, by Frieder Nake” doi:10.1145/1056224.1056234 For easiest access, paste the DOI into Sci-Hub. If that interestes you, check out his 2019 paper “Georg Nees & Harold Cohen: Re:tracing the origins of digital media”. ↩︎
-
The most common translation of “irrweg” appears to be the figurative “wrong path”—as in being on the wrong track, or leaving the straight and narrow—or a wandering or tortuous path. I find the idea of a computer procedure designed to be called repeatedly in a series, named elementary wrong path, delightful. ↩︎
